LeetCode
1
2
3
4
5
6
7class Solution {
public boolean containsDuplicate(int[] nums) {
Set<Integer> set=new HashSet<>();
for(int i:nums) set.add(i);
return nums.length!=set.size();
}
}
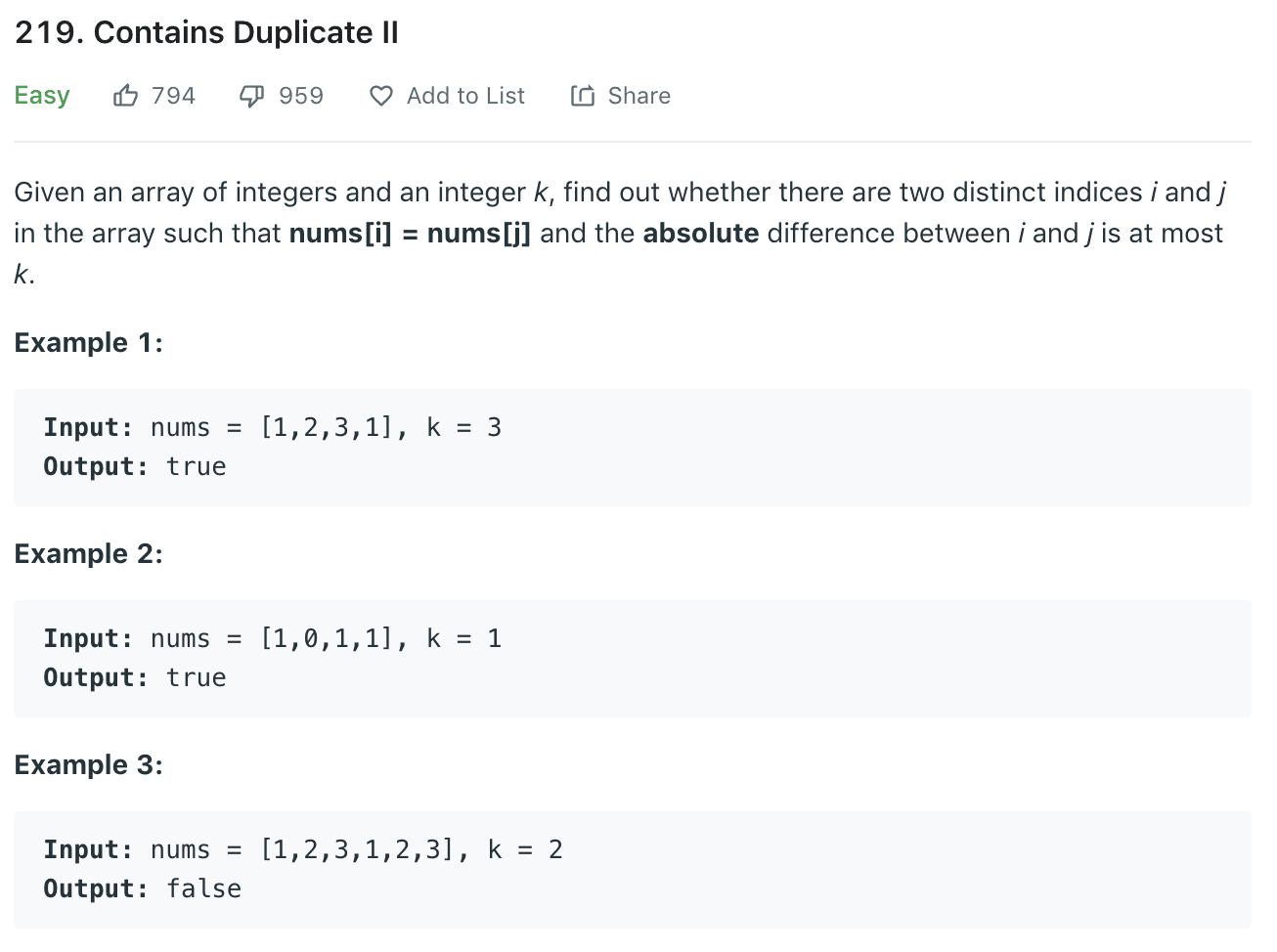
Approach #1 (Naive Linear Search): Time complexity : O(nmin(k,n))1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
for(int i=0;i<nums.length;i++){
for(int j=i+1;j<=i+k&&j<nums.length;j++){
if(nums[i]==nums[j]) return true;
}
}
return false;
}
}
// or
/*
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
for(int i=0;i<nums.length;i++){
for(int j=Math.max(i-k,0);j<i;j++){
if(Math.abs(nums[i]-nums[j])<=t) return true;
}
}
return false;
}
}*/
Approach #2 (Binary Search Tree): Time complexity : O(nlog(min(k,n)))1
2
3
4
5
6
7
8
9
10
11class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
Set<Integer> set=new TreeSet<>();
for(int i=0;i<nums.length;i++){
if(set.contains(nums[i])) return true;
set.add(nums[i]);
if(set.size()>k) set.remove(nums[i-k]);
}
return false;
}
}
Approach #3 (Hash Table)1
2
3
4
5
6
7
8
9
10
11class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
Set<Integer> set=new HashSet<>();
for(int i=0;i<nums.length;i++){
if(set.contains(nums[i])) return true;
set.add(nums[i]);
if(set.size()>k) set.remove(nums[i-k]);
}
return false;
}
}
LeetCode
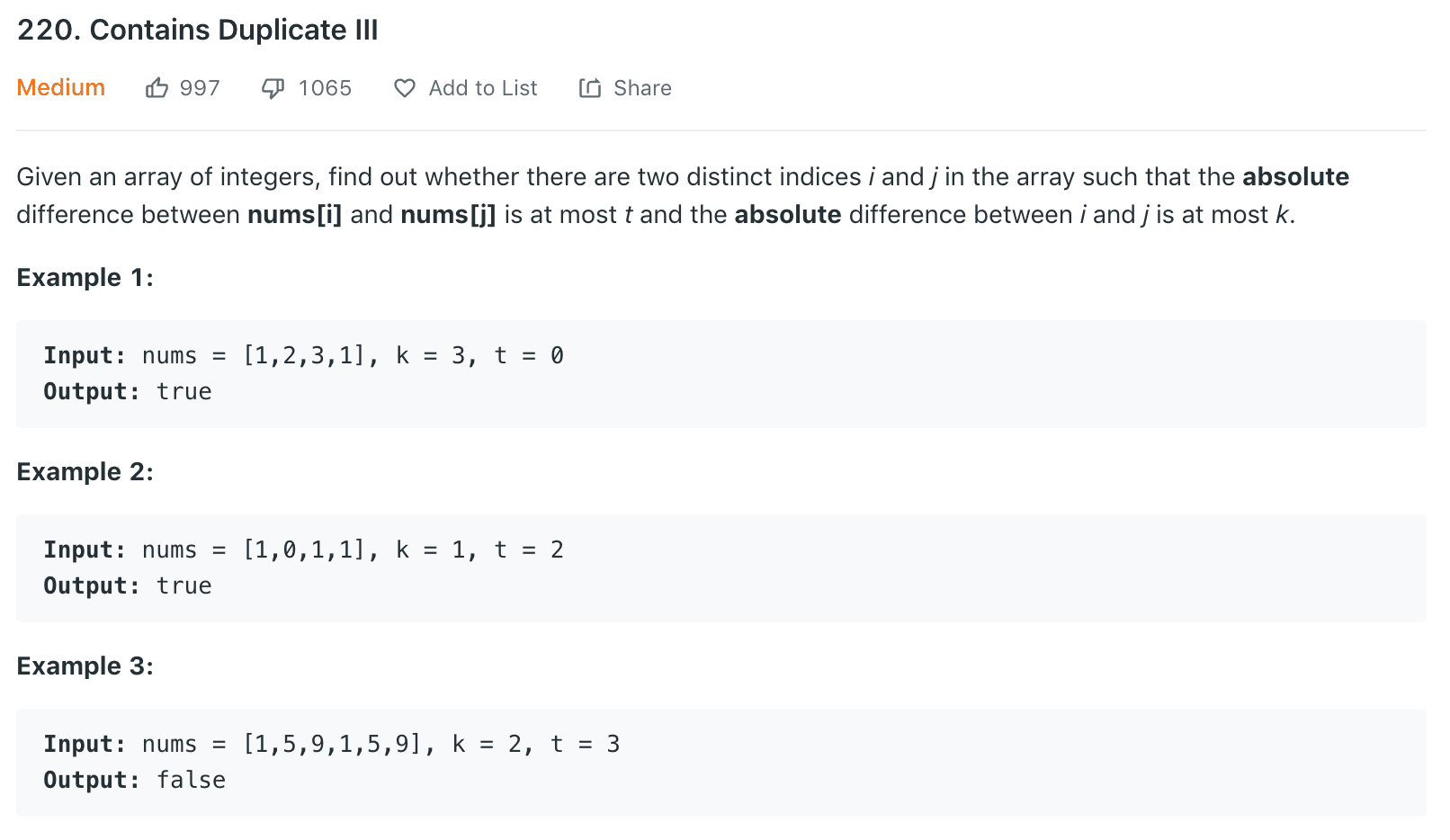
Approach #1 (Naive Linear Search) [Time Limit Exceeded]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution{
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
for (int i = 0; i < nums.length; ++i) {
for (int j = Math.max(i - k, 0); j < i; ++j) {
if (Math.abs((long)nums[i] - (long)nums[j]) <= (long)t) return true;
}
}
return false;
}
}
// Time limit exceeded.
/*
class Solution {
private int[] util(int i,int t){
int[] nearby=new int[2*t+1];
int m=0;
for(int j=i-t;j<=i+t;j++) nearby[m++]=j;
return nearby;
}
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
Set<Integer> set=new HashSet<>();
for(int i=0;i<nums.length;i++){
for(int j:util(nums[i],t)) if(set.contains(j)) return true;
set.add(nums[i]);
if(set.size()>k) set.remove(nums[i-k]);
}
return false;
}
}*/
Approach #2 (Binary Search Tree) [Accepted]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
TreeSet<Integer> set = new TreeSet<>();
for (int i = 0; i < nums.length; ++i) {
// Find the successor of current element
Integer s = set.ceiling(nums[i]);
if (s != null && (long)s-(long)nums[i] <= (long)t) return true;
// Find the predecessor of current element
Integer g = set.floor(nums[i]);
if (g != null && (long)nums[i]-(long)g <= (long)t) return true;
set.add(nums[i]);
if (set.size() > k) {
set.remove(nums[i - k]);
}
}
return false;
}
}
Approach #3 (Buckets) [Accepted]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27public class Solution {
// Get the ID of the bucket from element value x and bucket width w
// In Java, `-3 / 5 = 0` and but we need `-3 / 5 = -1`.
private long getID(long x, long w) {
return x < 0 ? (x + 1) / w - 1 : x / w;
}
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
if (t < 0) return false;
Map<Long, Long> d = new HashMap<>();
long w = (long)t + 1;
for (int i = 0; i < nums.length; ++i) {
long m = getID(nums[i], w);
// check if bucket m is empty, each bucket may contain at most one element
if (d.containsKey(m)) return true;
// check the neighbor buckets for almost duplicate
if (d.containsKey(m - 1) && Math.abs(nums[i] - d.get(m - 1)) < w)
return true;
if (d.containsKey(m + 1) && Math.abs(nums[i] - d.get(m + 1)) < w)
return true;
// now bucket m is empty and no almost duplicate in neighbor buckets
d.put(m, (long)nums[i]);
if (i >= k) d.remove(getID(nums[i - k], w));
}
return false;
}
}