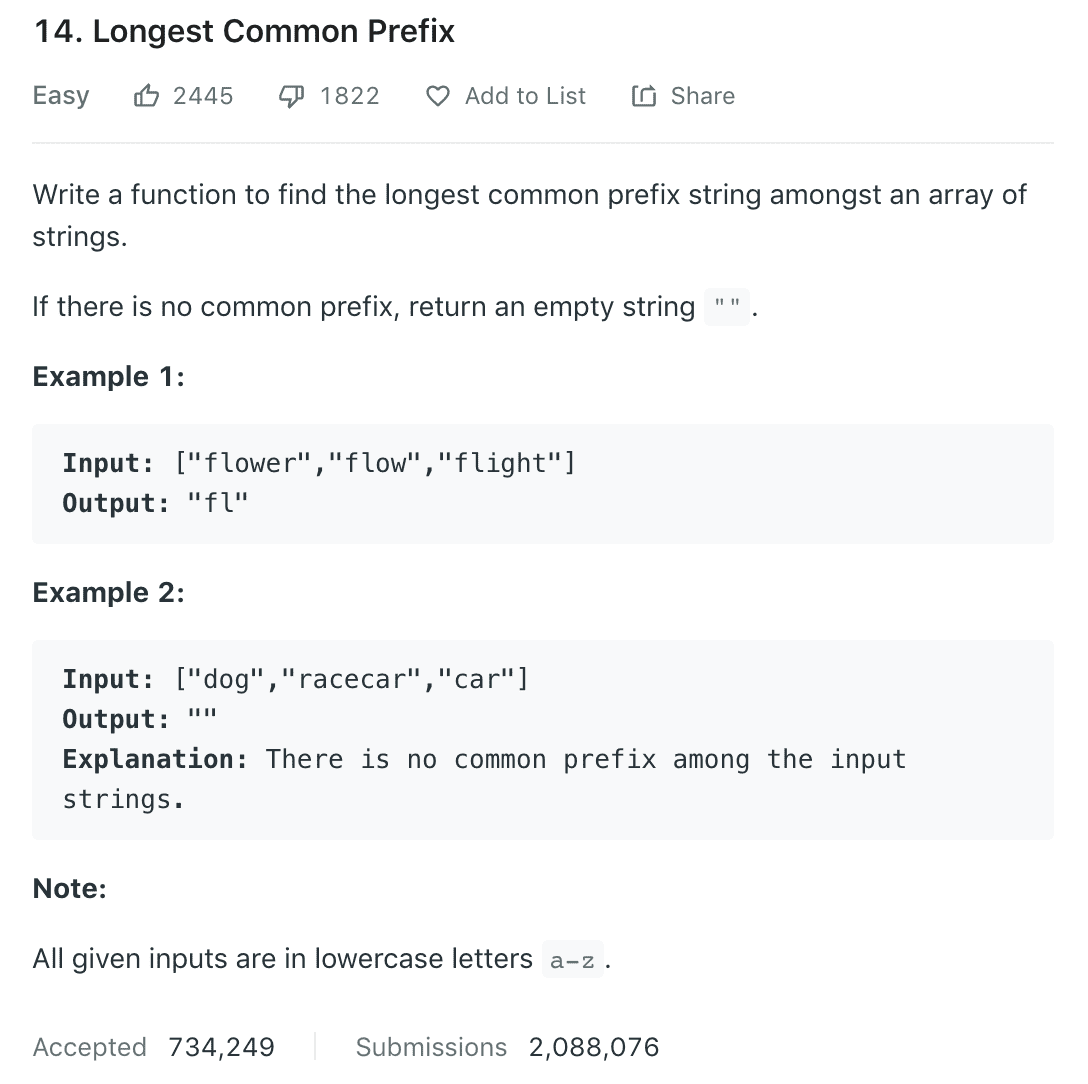
Approach 1: Horizontal scanning, Time complexity: O(S) , where S is the sum of all characters in all strings1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public String longestCommonPrefix(String[] strs) {
if(strs==null||strs.length==0) return "";
String prefix=strs[0];
for(int i=1;i<strs.length;i++){
while(strs[i].indexOf(prefix)!=0){
prefix=prefix.substring(0,prefix.length()-1);
if(prefix.length()==0) return "";
}
}
return prefix;
}
}
Approach 2: Vertical scanning, Time complexity: O(S) , where S is the sum of all characters in all strings1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
static String longestCommonPrefix(String[] strs) {
if(strs==null||strs.length==0) return "";
for(int i=0;i<strs[0].length();i++){
for(int j=1;j<strs.length;j++){
if(i==strs[j].length()||strs[0].charAt(i)!=strs[j].charAt(i))
return strs[0].substring(0,i);
}
}
return strs[0];
}
}
Approach 3: Divide and conquer, Time complexity: O(S), where S is the number of all characters in the array1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) return "";
return longestCommonPrefix(strs, 0, strs.length - 1);
}
private String longestCommonPrefix(String[] strs, int l, int r) {
if (l == r) {
return strs[l];
} else {
int mid = (l + r) / 2;
String lcpLeft = longestCommonPrefix(strs, l, mid);
String lcpRight = longestCommonPrefix(strs, mid + 1, r);
return commonPrefix(lcpLeft, lcpRight);
}
}
String commonPrefix(String left, String right) {
int min = Math.min(left.length(), right.length());
for (int i = 0; i < min; i++) {
if (left.charAt(i) != right.charAt(i)){
return left.substring(0, i);
}
}
return left.substring(0, min);
}
}
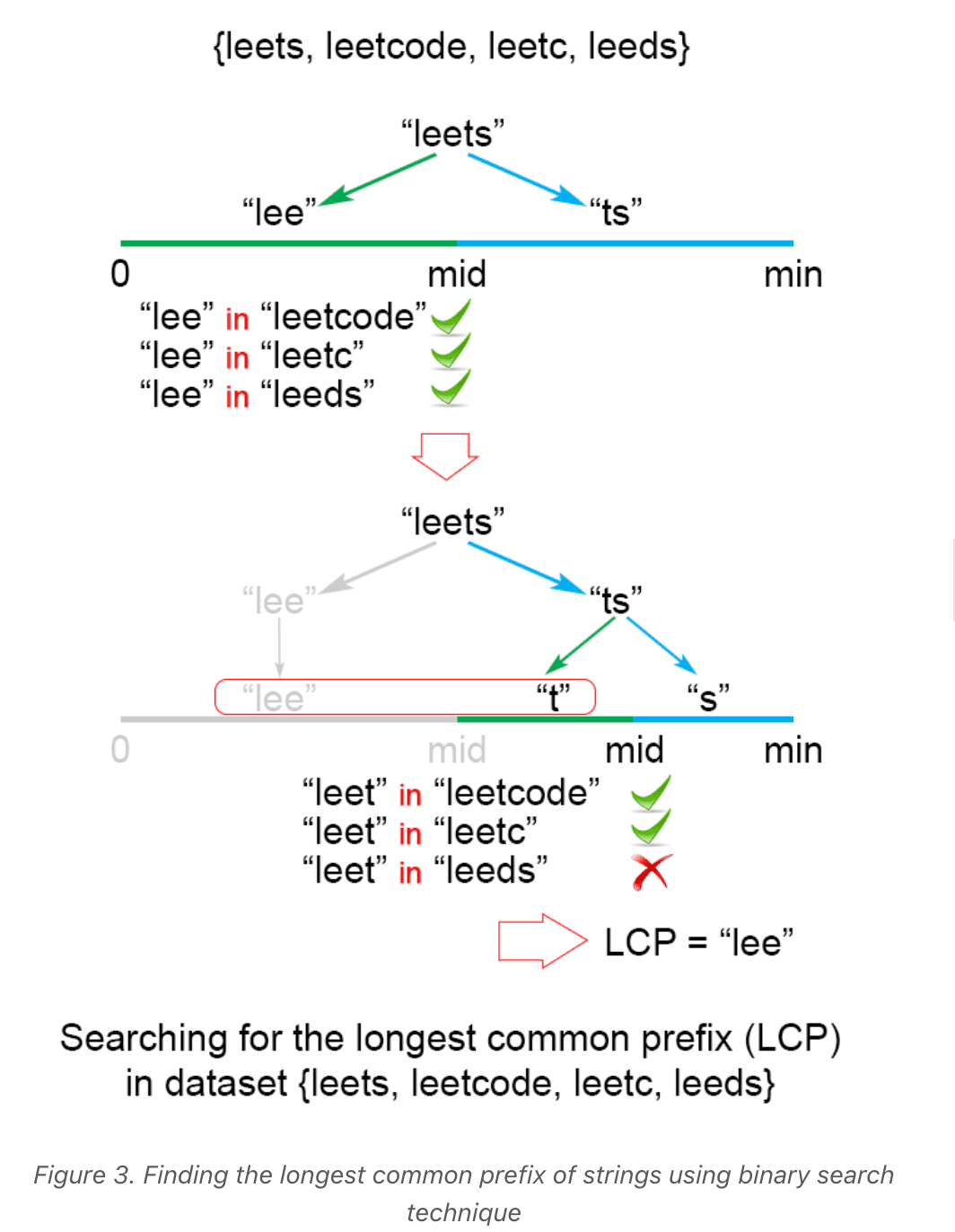
Approach 4: Binary search, Time complexity: O(S⋅logm)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) return "";
int minLen = Integer.MAX_VALUE;
for (String str : strs) minLen = Math.min(minLen, str.length());
int low = 1;
int high = minLen;
while (low <= high) {
int middle = (low + high) / 2;
if (isCommonPrefix(strs, middle))
low = middle + 1;
else
high = middle - 1;
}
return strs[0].substring(0, (low + high) / 2);
}
private boolean isCommonPrefix(String[] strs, int len) {
String str1 = strs[0].substring(0, len);
for (int i = 1; i < strs.length; i++)
if (!strs[i].startsWith(str1)) return false;
return true;
}
}
Approach 5: Prefix trie, Time complexity : O(S)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59class TrieNode{
final int ALPHABETA_SIZE=26;
TrieNode[] children=new TrieNode[ALPHABETA_SIZE];
boolean endOfWord;
TrieNode(){
endOfWord=false;
for(int i=0;i<ALPHABETA_SIZE;i++) children[i]=null;
}
}
class Trie{
static TrieNode root;
static void insert(String s){
int len=s.length();
TrieNode p=root;
for(int level=0;level<len;level++){
int idx=s.charAt(level)-'a';
if(p.children[idx]==null) p.children[idx]=new TrieNode();
p=p.children[idx];
}
p.endOfWord=true;
}
static String longestCommonPrefix(){
TrieNode p=root;
StringBuilder sb=new StringBuilder();
while(p!=null){
int[] check=cntChildren(p);
if(check[0]==1){
sb.append((char)('a'+check[1]));
p=p.children[check[1]];
}else{
break;
}
if(p.endOfWord) break;
}
return sb.toString();
}
static int[] cntChildren(TrieNode node){
int cnt=0,idx=0;
for(int i=0;i<26;i++){
if(node.children[i]!=null) {cnt++;idx=i;}
}
return new int[]{cnt,idx};
}
}
class Solution {
public String longestCommonPrefix(String[] strs) {
if(strs==null||strs.length==0) return "";
Trie.root=new TrieNode();
for(String s:strs){
if(s.isEmpty()) return "";
else Trie.insert(s);
}
return Trie.longestCommonPrefix();
}
}