23. Merge k Sorted Lists

Posted on | Edited on | Views:

LeetCode

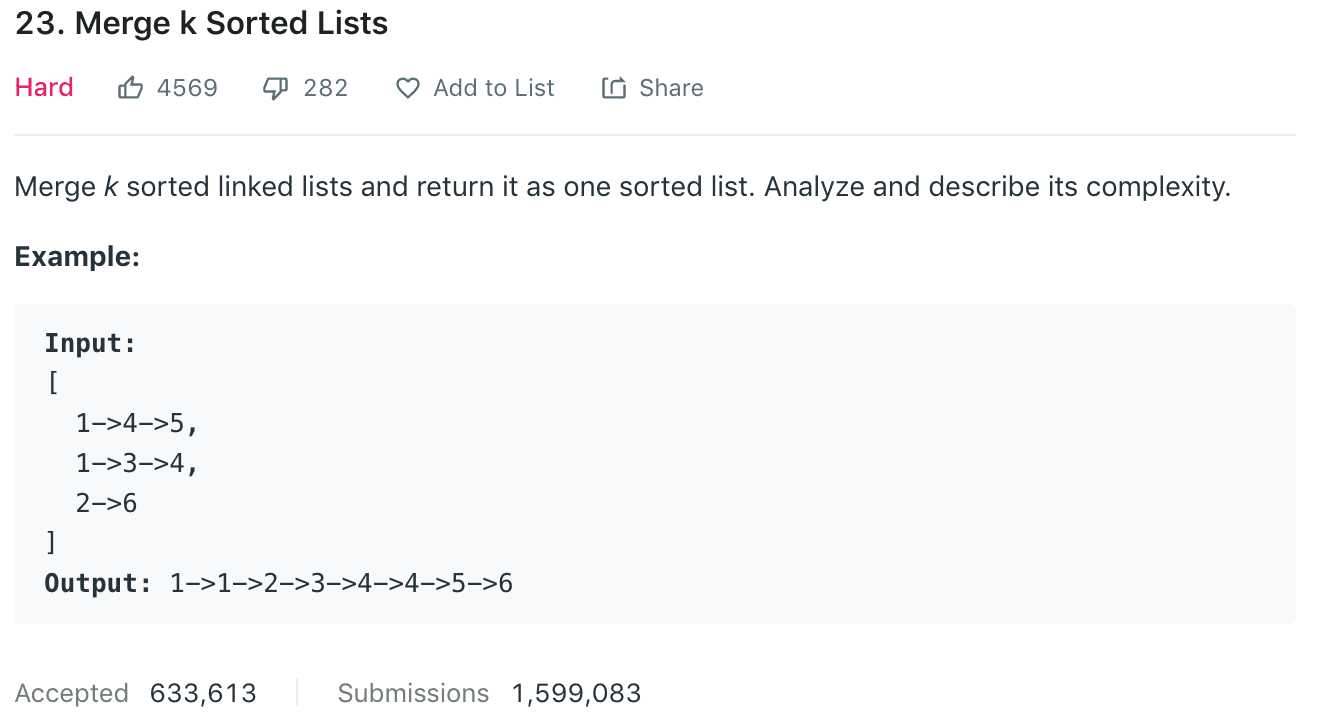
Approach 1: Brute Force, Time complexity: O(NlogN) where NN is the total number of nodes.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        List<Integer> ls=new ArrayList();
        for (ListNode node:lists){
            while(node!=null){
                ls.add(node.val);
                node=node.next;
            }
        }
        Collections.sort(ls);
        ListNode dummyHead=new ListNode(-1);
        ListNode ans=dummyHead;
        for(int val:ls){
            ans.next=new ListNode(val);
            ans=ans.next;
        }
        return dummyHead.next;
    }
}

Approach 2: Compare one by one, Time complexity: O(kN) where k is the number of linked lists

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        ListNode head=new ListNode(-1);
        ListNode dummy=head;     
        while(true){
            int minVal=Integer.MAX_VALUE;
            boolean isLoop=true;
            int minIdx=-1;          
            for(int i=0;i<lists.length;i++){
                if(lists[i]!=null && lists[i].val<=minVal){
                    minVal=lists[i].val;
                    minIdx=i;
                    isLoop=false;
                }              
            }
            if(isLoop) break;
            
            dummy.next=lists[minIdx];
            dummy=dummy.next;
            lists[minIdx]=lists[minIdx].next;
        } 
        return head.next;
    }
}

Approach 3: Optimize Approach 2 by Priority Queue, Time complexity: O(Nlogk) where k is the number of linked lists. link

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if(lists==null || lists.length==0) return null;
        PriorityQueue<ListNode> pq=new PriorityQueue<>(lists.length,(a,b)->a.val-b.val);
        for(ListNode node:lists){
            if(node!=null) pq.offer(node);
        } 
        
        ListNode preHead=new ListNode(-1),p=preHead;
        while(!pq.isEmpty()){
            p.next=pq.poll();
            p=p.next;
            if(p.next!=null) pq.offer(p.next);
        }
        
        return preHead.next;
    }
}

Approach 4: Merge with Divide And Conquer, Time complexity: O(Nlogk) where k is the number of linked lists.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        return merge(lists,0,lists.length-1);
    }
    public ListNode merge(ListNode[] lists,int lo,int hi){
        if(lo==hi) return lists[lo];
        if(lo<hi){
            int mid=(lo+hi)/2;
            ListNode l1=merge(lists,lo,mid);
            ListNode l2=merge(lists,mid+1,hi);
            return mergeTwoLists(l1,l2);
        }
        return null;
    }
    public ListNode mergeTwoLists(ListNode l1,ListNode l2){
        if(l1==null) return l2;
        else if(l2==null) return l1;
        if(l1.val<l2.val) {l1.next=mergeTwoLists(l1.next,l2);return l1;}
        else {l2.next=mergeTwoLists(l1,l2.next);return l2;}
    }
}

0%