29. Divide Two Integers

LeetCode

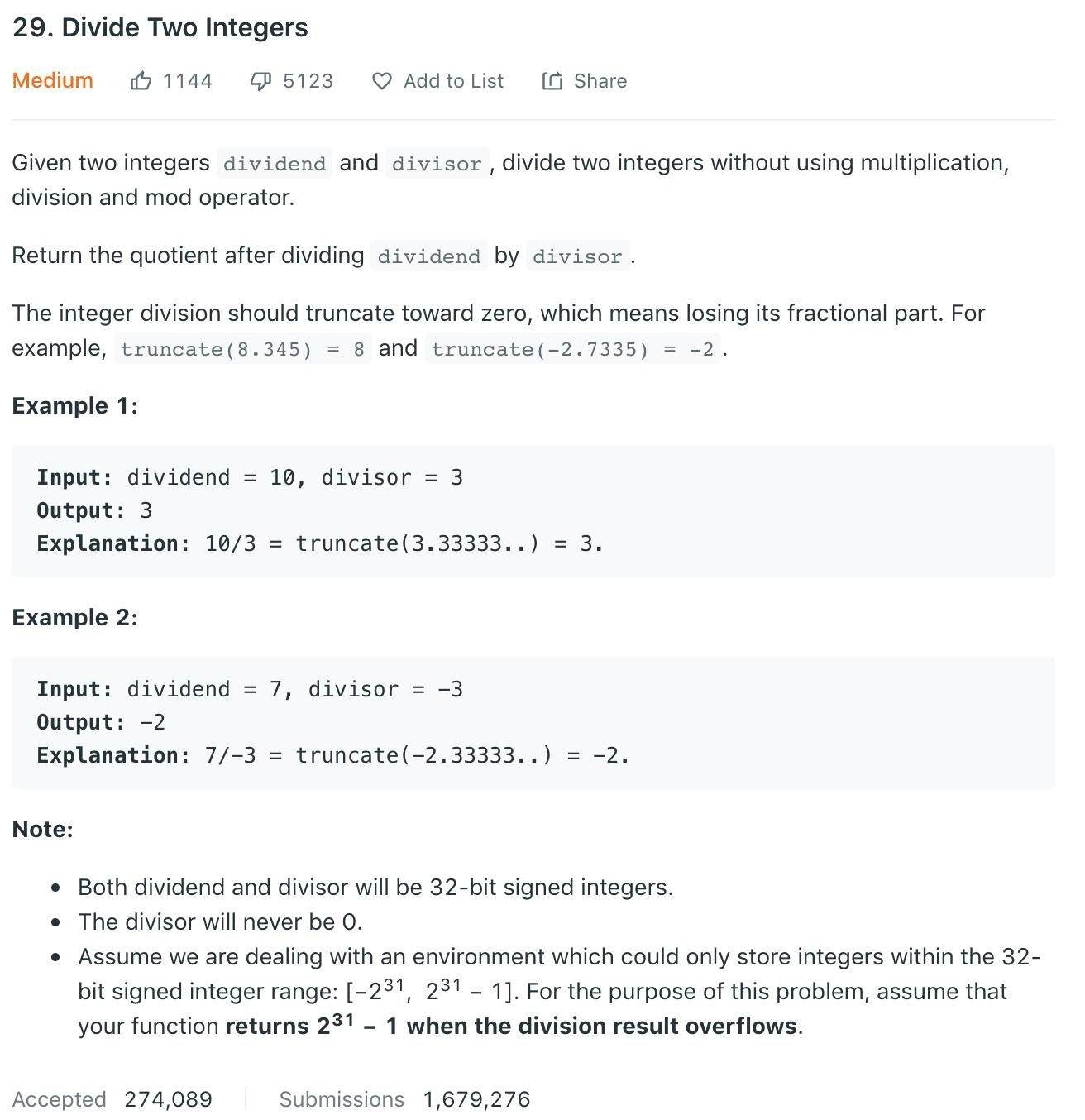
Approach 1: Repeated Subtraction (brute-force), Time Complexity: O(n), 2483ms, Space Complexity: O(1)

class Solution {
    public int divide(int dividend, int divisor) {
        // special case: overflow
        if(dividend==Integer.MIN_VALUE && divisor==-1) return Integer.MAX_VALUE;
        
        /* We need to convert both numbers to negatives
         * for the reasons explained above.
         * Also, we count the number of negatives signs. */
        int negativeNum=2;
        if(dividend>0) {negativeNum--;dividend=-dividend;}
        if(divisor>0) {negativeNum--;divisor=-divisor;}
        
        /* Count how many times the divisor has to be subtracted
         * to get the dividend. This is the quotient. */
        int quotient=0;
        while(dividend<=divisor){
            quotient++;
            dividend-=divisor;
        }
        
        /* If there was originally one negative sign, then
         * the quotient is negative.*/
        if(negativeNum==1) quotient=-quotient;
        
        return quotient;
    }
}

Approach 2: Repeated Exponential Searches, Time Complexity: O(log^2N), 1ms, Space Complexity: O(1)

This algorithm is known as exponential search and is commonly used for searching sorted spaces of unknown size for the first value that past a particular condition. It it a lot like binary search, having the same time complexity of O(logn)

class Solution {
    public int divide(int dividend, int divisor) {
        if(dividend==Integer.MIN_VALUE&&divisor==-1) return Integer.MAX_VALUE;
        
        final int HALF_MIN_VALUE=Integer.MIN_VALUE>>1;
        
        int negativeNum=2;
        if(dividend>0) {negativeNum--;dividend=-dividend;}
        if(divisor>0) {negativeNum--;divisor=-divisor;}
        
        int quotient=0;
        while(dividend<=divisor){
            int pwrOf2=-1;
            int value=divisor;
            
            while(value>=HALF_MIN_VALUE && value+value>=dividend){
                value+=value;
                pwrOf2+=pwrOf2;
            }
            
            quotient+=pwrOf2;
            dividend-=value;
        }
        
        if(negativeNum!=1) quotient=-quotient;
        
        return quotient;
    }
}

Approach 3: Adding Powers of Two, Time Complexity: O(logn), Space Complexity: O(logn)

class Pair{
    int doubles;
    int pwrOf2;
    Pair(int doubles,int pwrOf2) {this.doubles=doubles;this.pwrOf2=pwrOf2;}
    int getDoubles() {return doubles;}
    int getPwrOf2() {return pwrOf2;}
}
class Solution {
    public int divide(int dividend, int divisor) {
        if(dividend==Integer.MIN_VALUE && divisor==-1) return Integer.MAX_VALUE;
        
        final int HALF_MIN_VALUE=Integer.MIN_VALUE>>1;
        
        int negativeNum=2;
        if(dividend>0) {negativeNum--;dividend=-dividend;}
        if(divisor>0) {negativeNum--;divisor=-divisor;}
        
        LinkedList<Pair> ls=new LinkedList<>();
        int pwrOf2=-1;
        while(divisor>=dividend){
            ls.add(new Pair(divisor,pwrOf2));
            if(divisor<HALF_MIN_VALUE) break;
            divisor+=divisor;
            pwrOf2+=pwrOf2;
        }
        
        int quotient=0;
        for(int i=ls.size()-1;i>=0;i--){
            if(ls.get(i).getDoubles()>=dividend){
                quotient+=ls.get(i).getPwrOf2();
                dividend-=ls.get(i).getDoubles();
            } 
        }
        
        if(negativeNum!=1) quotient=-quotient;
        
        return quotient;
    }
}

Approach 4: Adding Powers of Two with Bit-Shifting, Time Complexity: O(logn), Space Complexity: O(1)

class Solution {
    public int divide(int dividend, int divisor) {
        if(dividend==Integer.MIN_VALUE && divisor==-1) return Integer.MAX_VALUE;
        
        final int HALF_MIN_VALUE=Integer.MIN_VALUE>>1;
        
        int negativeNum=2;
        if(dividend>0) {negativeNum--;dividend=-dividend;}
        if(divisor>0) {negativeNum--;divisor=-divisor;}
        
        int highestDouble=divisor;
        int highestPwrOf2=-1;
        while(highestDouble>=HALF_MIN_VALUE&&highestDouble+highestDouble>=dividend){
            highestDouble+=highestDouble;
            highestPwrOf2+=highestPwrOf2;
        }
        
        int quotient=0;
        while(divisor>=dividend){
            if(highestDouble>=dividend){
                quotient+=highestPwrOf2;
                dividend-=highestDouble;
            }
            highestPwrOf2>>=1;
            highestDouble>>=1;
        }
        
        if(negativeNum!=1) quotient=-quotient;
        
        return quotient;
    }
}

Approach 5: Binary Long Division, Time Complexity: O(logn), Space Complexity: O(1)

class Solution {
    public int divide(int dividend, int divisor) {
        if(dividend==Integer.MIN_VALUE && divisor==-1) return Integer.MAX_VALUE;
        
        final int HALF_MIN_VALUE=Integer.MIN_VALUE>>1;
        
        int negativeNum=2;
        if(dividend>0) {negativeNum--;dividend=-dividend;}
        if(divisor>0) {negativeNum--;divisor=-divisor;}
        
        int maxBit=0;
        while(divisor>=HALF_MIN_VALUE&&divisor+divisor>=dividend){
            maxBit+=1;
            divisor+=divisor;
        }
        
        int quotient=0;
        for(int bit=maxBit;bit>=0;bit--){
            if(divisor>=dividend){
                quotient-=1<<bit;
                dividend-=divisor;
            }
            divisor=(divisor+1)>>1;
        }
        
        if(negativeNum!=1) quotient=-quotient;
        
        return quotient;
    }
}