42. Trapping Rain Water

Posted on | Edited on | Views:

LeetCode

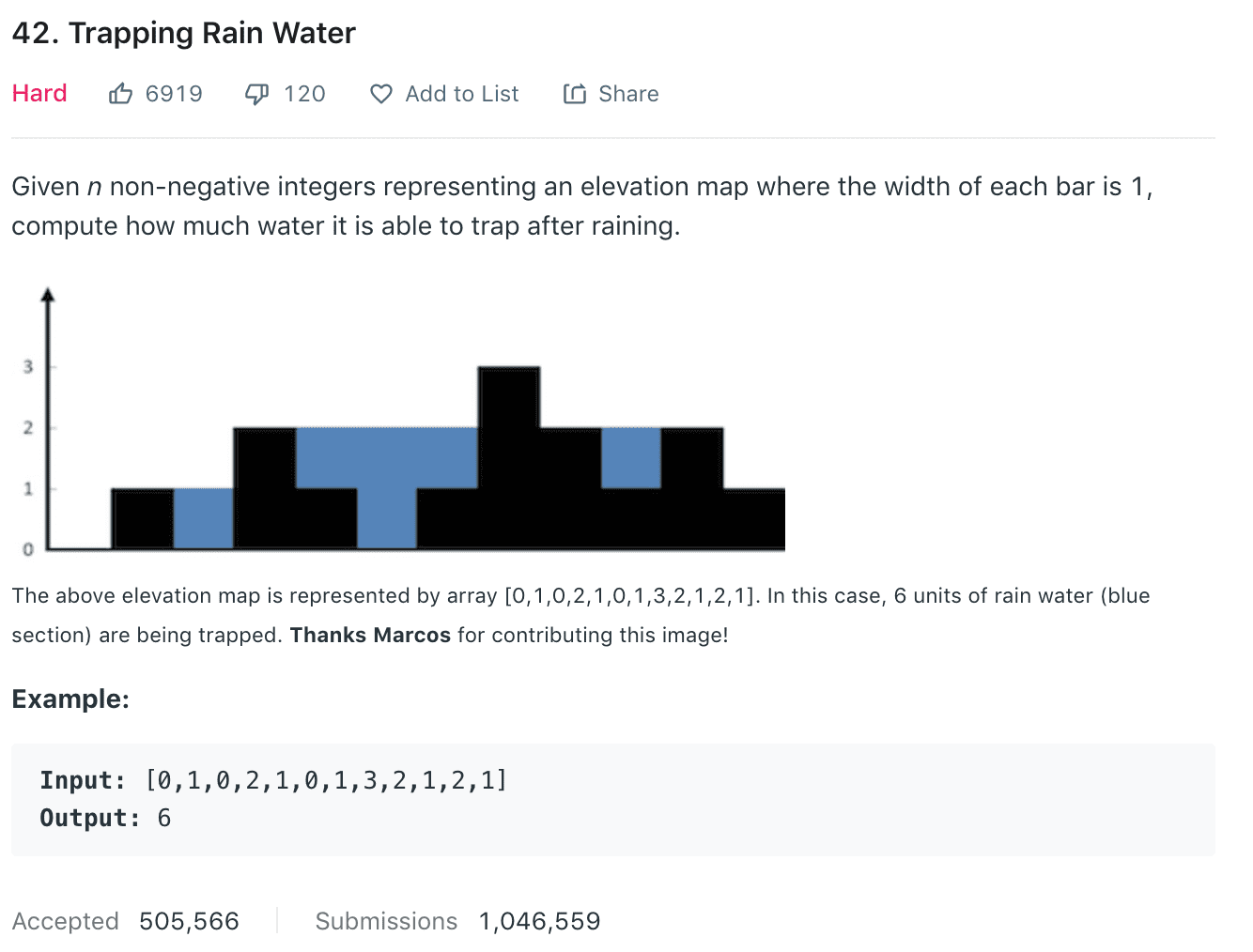
Approach 1: Brute force, Time complexity: O(n^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int trap(int[] height) {
        int ans=0;
        for(int i=0;i<height.length;i++){
            int left_max=0,right_max=0;
            int m=i,n=i;
            while(m>=0) left_max=Math.max(left_max,height[m--]);
            while(n<=height.length-1) right_max=Math.max(right_max,height[n++]);
            // System.out.println(height[i]+", left_max: "+left_max+", right_max: "+right_max+
            //                    ", capacity: "+ (Math.min(left_max,right_max)-height[i]));
            ans+=Math.min(left_max,right_max)-height[i];
        }
        return ans;
    }
}


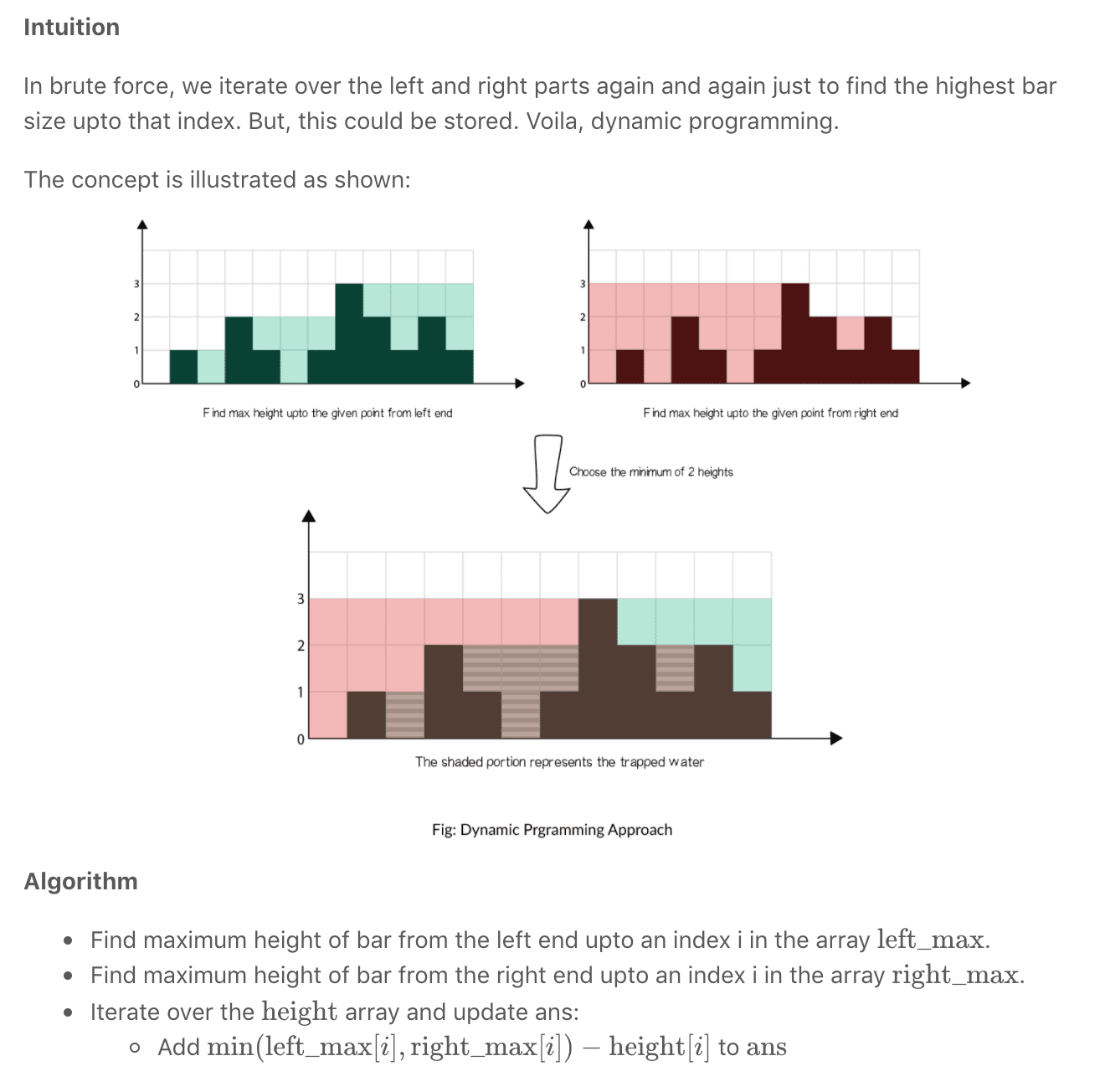
Approach 2: Dynamic Programming, Time complexity: O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int trap(int[] height) {
        if(height==null||height.length==0) return 0;
        
        int ans=0,size=height.length;
        int[] left_max=new int[size],right_max=new int[size];
        
        left_max[0]=height[0];
        for(int i=1;i<size;i++){
            left_max[i]=Math.max(height[i],left_max[i-1]);
        }
        
        right_max[size-1]=height[size-1];
        for(int i=size-2;i>=0;i--){
            right_max[i]=Math.max(height[i],right_max[i+1]);
        }
        
        for(int i=0;i<size;i++){
            ans+=Math.min(left_max[i],right_max[i])-height[i];
        }
        
        return ans;
    }
}

Approach 3: Using stacks, Time complexity: O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int trap(int[] height) {
        int ans=0,curr=0;
        LinkedList<Integer> stack=new LinkedList<>();
        while(curr<height.length){
            while(!stack.isEmpty()&& height[curr]>height[stack.peek()]){
                int top=stack.pop();
                if(stack.isEmpty()) break;
                int distance=curr-stack.peek()-1;
                int boundedHeight=Math.min(height[curr],height[stack.peek()])-height[top];
                ans+=distance*boundedHeight;
            }
            stack.push(curr++);
        }
        return ans;
    }
}

Approach 4: Using 2 pointers, Time complexity: O(n), Space complexity: O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int trap(int[] A) {
        int left=0,right=A.length-1;
        int res=0;
        int maxleft=0, maxright=0;
        while(left<right){
            if(A[left]<=A[right]){
                if(A[left]>=maxleft) maxleft=A[left];
                else res+=maxleft-A[left];
                left++;
            }else{
                if(A[right]>=maxright) maxright= A[right];
                else res+=maxright-A[right];
                right--;
            }
        }
        return res;
    }
}

0%