Amazon | OA 2019 | Critical Routers

Posted on | Edited on | Views:

link


REF. Connected Components in an undirected graph

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
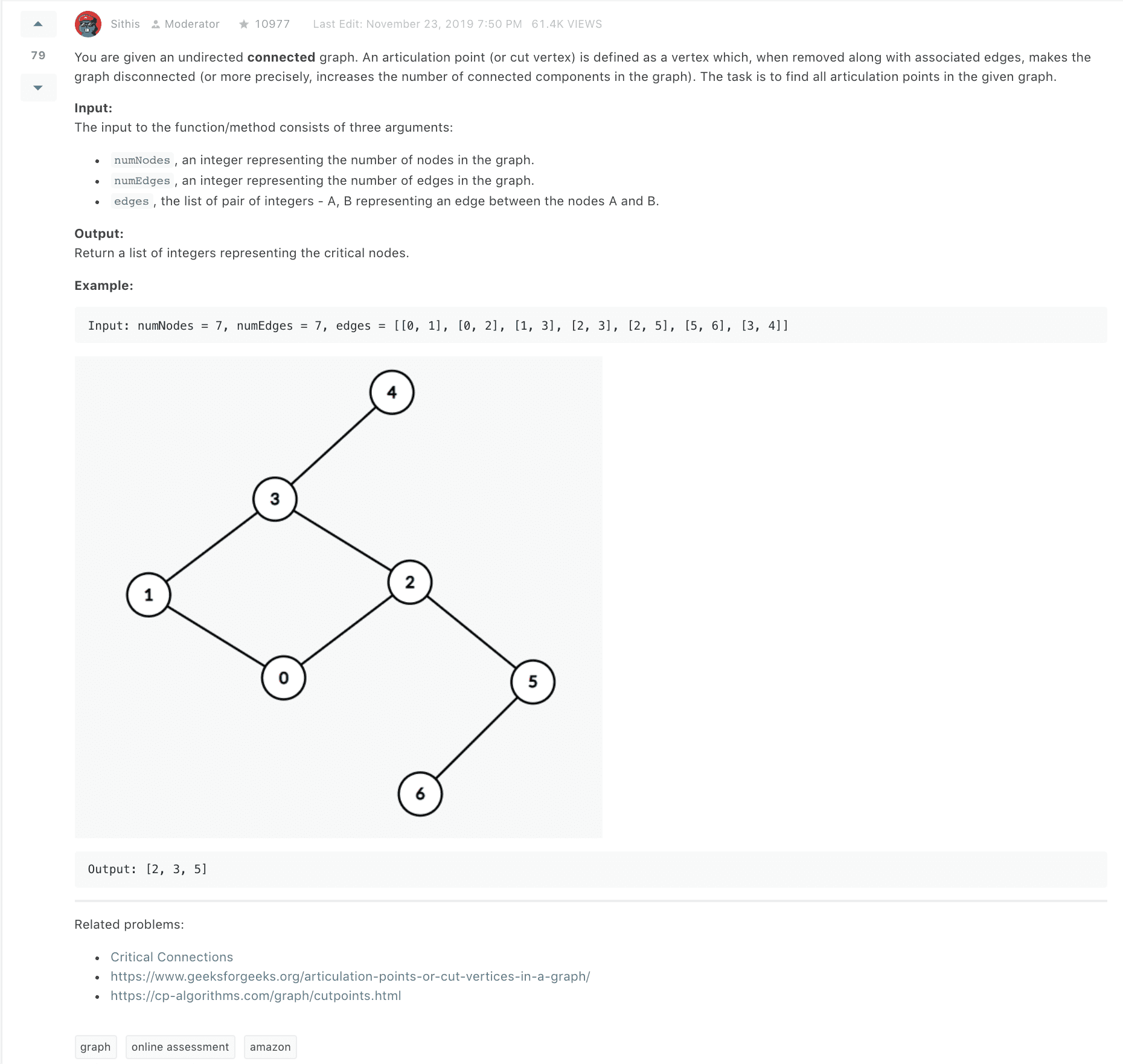
73
74
import java.util.*;

class Graph {

    int V;
    LinkedList<Integer>[] adjListArray;

    Graph(int V) {
        this.V = V;
        adjListArray = new LinkedList[V];
        for (int i = 0; i < V; i++) {
            adjListArray[i] = new LinkedList<Integer>();
        }
    }

    void addEdge(int src, int dest) {
        adjListArray[src].add(dest);
        adjListArray[dest].add(src);
    }

    void DFSUtil(int v, boolean[] visited) {
        visited[v] = true;
        // System.out.print(v + " ");
        for (int x : adjListArray[v]) {
            if (!visited[x]) DFSUtil(x, visited);
        }
    }

    int connectedComponents(int exclode, boolean sign) {
        int num=0;
        boolean[] visited = new boolean[V];
        for (int v = 0; v < V; ++v) {
            if (!sign&&!visited[v]) {
                DFSUtil(v, visited);
                num++;
            }else if(sign&&v!=exclode&&!visited[v]){
                DFSUtil(v, visited);
                num++;
            }
        }
        return num;
    }
}

public class MyClass {
    public static void main(String[] args) {
        int numNodes = 7;
        int[][] edges= {{0, 1}, {0, 2}, {1, 3}, {2, 3}, {2, 5}, {5, 6}, {3, 4}};
        Graph g = new Graph(numNodes);
        for(int[] edge:edges){
            g.addEdge(edge[0], edge[1]);
        }

        int beforeNum=g.connectedComponents(-1,false);
        System.out.println("connected components numbers: "+beforeNum+"\n");

        List<Integer> res=new ArrayList<>();
        for(int i=0;i<numNodes;i++){
            LinkedList<Integer> neighbors=g.adjListArray[i];
            for(int neighbor:neighbors){
                g.adjListArray[neighbor].remove((Object)i);
            }

            int afterNum=g.connectedComponents(i,true);
            System.out.println("connected components numbers: "+afterNum);
            if(afterNum>beforeNum) res.add(i);

            for(int neighbor:neighbors){
                g.adjListArray[neighbor].add(i);
            }
        }
        System.out.println(res);
    }
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/*
    A simple brute force solution,
    for every vertex, remove the corresponding edges and perform dfs.
    If total vertices traversed in dfs != numNodes-1,
    then the current removed vertex is a critical router.
*/
/*
class CriticalRouter {
    public List<Integer> getCriticalRouters(int numNodes, int numEdges, int[][] edges) {

        // construct graph
        Map<Integer, Set<Integer>> graph = new HashMap<>();

        // initialize graph
        for (int i = 0; i < numNodes; i++) graph.put(i, new HashSet<>());

        // add edges to graph
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];

            graph.get(u).add(v);
            graph.get(v).add(u);
        }

        List<Integer> result = new ArrayList<>();

        // calculate critical routers
        for (int nodeToRemove = 0; nodeToRemove < numNodes; nodeToRemove++) {

            // remove each node and its edges and check if entire graph is connected
            Set<Integer> nodeEdges = graph.get(nodeToRemove);
            int source = 0;
            for (int edge : nodeEdges) {
                graph.get(edge).remove(nodeToRemove);
                source = edge;
            }

            HashSet<Integer> visited = new HashSet<>();
            dfs(graph, source, visited);

            if (visited.size() != numNodes - 1) {
                // this node was a critical router
                result.add(nodeToRemove);
            }

            // add the edges back
            for (int edge : nodeEdges) graph.get(edge).add(nodeToRemove);
        }
        return result;
    }

    public void dfs(Map<Integer, Set<Integer>> graph, int source, Set<Integer> visited) {
        if(visited.contains(source)) return;
        visited.add(source);
        for (int child : graph.get(source)) dfs(graph, child, visited);
    }
}*/

0%