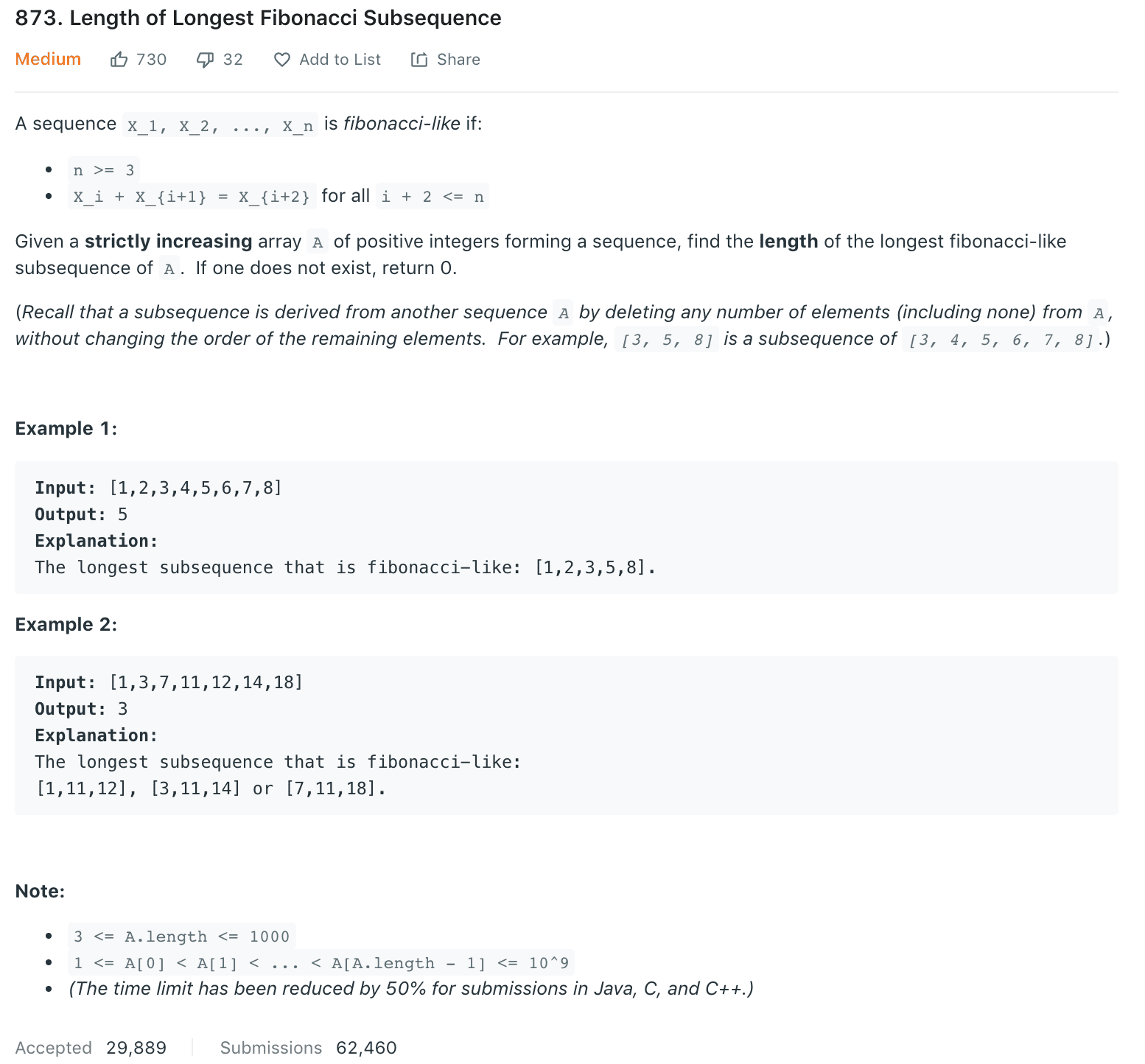
Approach 1: Brute Force with Set1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46// Iterative
class Solution {
public int lenLongestFibSubseq(int[] A) {
int len=A.length;
Set<Integer> set=new HashSet<>();
for(int i:A) set.add(i);
int ans=0;
for(int i=0;i<len;i++){
for(int j=i+1;j<len;j++){
int x=A[j],y=A[i]+A[j];
int length=2;
while(set.contains(y)){
int tmp=y;
y+=x;
x=tmp;
ans=Math.max(ans,++length);
}
}
}
return ans>2?ans:0;
}
}
/* Recursive
class Solution {
private int dfs(int i,int j,int len,Set<Integer> set){
if(!set.contains(i+j)) return 0;
return Math.max(len,dfs(j,i+j,len+1,set));
}
public int lenLongestFibSubseq(int[] A) {
int len=A.length;
Set<Integer> set=new HashSet<>();
for(int i:A) set.add(i);
int ans=0;
for(int i=0;i<len;i++){
for(int j=i+1;j<len;j++){
ans=Math.max(ans,dfs(A[i],A[j],3,set));
}
}
return ans>2?ans:0;
}
}*/
Approach 2: Dynamic Programming
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public int lenLongestFibSubseq(int[] A) {
int len=A.length;
Map<Integer,Integer> index=new HashMap<>();
for(int i=0;i<len;i++) index.put(A[i],i);
Map<Integer,Integer> longest=new HashMap<>();
int ans=0;
for(int k=0;k<len;k++){
for(int j=0;j<k;j++){
int i=index.getOrDefault(A[k]-A[j],-1);
if(i>=0&&i<j){
longest.put(j*len+k,longest.getOrDefault(i*len+j,2)+1);
ans=Math.max(ans,longest.get(j*len+k));
}
}
}
return ans>=3?ans:0;
}
}
link
DP1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26// Time Complexity: O(N^2)
// Space Complexity: O(N^2)
class Solution {
public int lenLongestFibSubseq(int[] A) {
int n = A.length;
int max = 0;
int[][] dp = new int[n][n];
for (int i = 2; i < n; i++) {
int l = 0, r = i - 1;
while (l < r) {
int sum = A[l] + A[r];
if (sum > A[i]) {
r--;
} else if (sum < A[i]) {
l++;
} else {
dp[r][i] = dp[l][r] + 1;
max = Math.max(max, dp[r][i]);
r--;
l++;
}
}
}
return max == 0 ? 0 : max + 2;
}
}